A Beginner's Guide to Vectorization By Hand: Part 1
The CPU vendors have been trying for a lot of time to exploit as much parallelism as they can and the introduction of vector instructions is one way to go. While compiler writers try their best to provide automatic vectorization, there's a lot of ground to cover. Until we get there, this a series of tutorials to help you approach vectorization yourself with some common patterns.
In short, it is the act of using (effectively) SIMD (Single-Instruction Multiple-Data) instructions. "Regular" instructions operate on single data, which you can think as operating at steps of single values. For example, an addition instruction gets as input two registers, each of which contains a single value. It then adds their values and produces one single value for the output register. A SIMD addition instruction would get as input two e.g. quadruple registers (each register contains 4 actual values), would add them (element-wise) and produce 4 values (in one register, the output register).
These instructions and registers are usually called "wide" or "vector" instructions / registers (which is why you may see vectorization being referred as widening), while the regular counterparts are called scalar. The key is that these vector instructions run at the same speed of the scalar instructions. This means that if you can get your algorithm to operate on multiple data and you have instructions that say can operate on 4 values at a time, you can (theoretically) speed up your code by a factor of 4.
The easiest thing to vectorize is a single addition. Let's say we have this function:
int add(int a, int b) { return a + b; }
This function obviously operates on scalar values, that is, int. We would like
to convert it to operate at 4 ints at a time, so, a
and b should have 4 (packed) int values (so each would be e.g. 128 bits in size) and the function should also return such a 4-packed value. Assuming there's a type int4
that captures these "4 packed values" semantics, it would look something like this:
int4 add4(int4 a, int4 b) { return a + b; }
There are a couple of problems here. First, there's no int4, but even if there was, C does not
define the + operator for int4 operands. We would basically
have to create a new language that understands such types and a compiler that generates the relevant instructions. Although
such attempts exist, this is not the most common way because most people still
want to write in the language they know, which is usually C or C++.
The currently used workaround was introduced by Intel, I believe, and it is two-fold. First, it defined types like
int4, but with worse names. Then, it provided intrinsic functions for any operation
that we might want to do (actually I mean: any operation that the hardware provides)
on values of such types. On the surface, these are C-like functions which though
are translated, 1-to-1, to specific vector instructions by the compiler. And they have even worse names.
As you can imagine, since there are hundreds of instructions, there are hundreds of intrinsics. Also, since we write directly the CPU instructions we want to use, this is quite some low-level programming, with the compiler doing minimal optimizations (e.g., usually some basic register allocation). Our best friend here is the Intel Intrinsics Guide.
The real-world version of the function above is the following:
__m128i add4(__m128i a, __m128i b) { return _mm_add_epi32(a, b); }
__m128i is a type whose values are 128 bits and they're supposed to be used as integers. The intrinsic
I used, which corresponds to the add operations of 4 packed values is _mm_add_epi32().
There's something important here: A __m128i vector means just that it is a 128-bit integer. You have
to then specify in the instruction how do you want it to be treated. Such a vector can be treated as two 64-bit integers,
four 32-bit integers, eight 16-bit integers or sixteen 8-bit integers. It can also be treated as signed or unsigned. You
can see now why if you search the intel intrinsics guide for an addition on __m128i you'll
see a lot of intrinsics.
The specific intrinsic we used ends with _epi32 which means
treat the inputs as four 32 bit (packed) integers (the four is omitted because it is implied as 128 / 32 since the inputs are 128-bits)
and also return such a value.
In general, if you want to vectorize code, you always start by thinking what you want the hardware to do. And then you search
the intel intrinsics guide for e.g. _mm_add. I wouldn't recommend memorizing all the intrinsics
deliberately, rather that will happen as you use them. However, it's good to remember some basic concepts, like
what epi8/16/32/64 mean
or that si128 means to treat the inputs as whole 128-bit values.
So, ok, we just vectorized an addition but what if we want to vectorize a whole loop of additions. For example, we might have a function that gets two arrays A and B, adds each of their elements and stores the result to an array C. The scalar version would like this:
void sum_arrays(int *A, int *B, int *C, int len) { for (int i = 0; i < len; ++i) C[i] = A[i] + B[i]; }
Given that we have vectorized a single add, it shouldn't be too hard. The obvious way to approach it is instead of doing one addition at every iteration to do 4 of them. In pseudocode, it would look like this:
void sum_arrays(int *A, int *B, int *C, int len) { for (int i = 0; i < len; i += 4) { v1 = load 4 values from A v2 = load 4 values from B res = 4-packed add(v1, v2) store res (which is 4 values) in C } }
Note the i += 4 there. We're moving in steps of 4 in every iteration (you could also
think of it as doing 4 iterations at once in every widened iteration, but this is somewhat less precise).
The first important thing we haven't seen yet is how to load from and store to memory. A 128-bit load can be issued with the intrinsic _mm_loadu_si128 (__m128i const *mem_addr).
Note that this function gets a __m128i const * pointer, so you can't just pass
A to it unless you cast it. This is enforced supposedly for "safety reasons" which
honestly, is kind of funny when you're one step before (inline) assembly.
And it is usually irritating because for a lot of people, including me, it is easier to still think in scalar pointer arithmetic in the vectorized version. So, I usually create wrappers for the store and load that get
void * for the memory argument which means you can pass whatever to it.
__m128i loadu_si128(void *m) { return _mm_loadu_si128((const __m128i*) m); }
Similarly, to store 4 values at a time (or 128 bits), so we can use (a wrapper version of) the intrinsic void _mm_storeu_si128 (__m128i* mem_addr, __m128i a)
Now, and using our previous add4() function, we're closer to the final thing:
void sum_arrays(int *A, int *B, int *C, int len) { for (int i = 0; i < len; i += 4) { __m128i v1 = loadu_si128(&A[i]); __m128i v2 = loadu_si128(&B[i]); __m128i res = add4(v1, v2); store_si128(&C[i], res); } }
The vectorization above will do its job... most of the time. But it is not actually semantically equivalent to the original loop. It turns out that moving in bigger steps results in different behavior some of the time. Let's see why.
First of all, what if len is not a multiple of 4 ? Imagine that it is say 5.
Then, we're going to do two iterations of steps of 4. The first will be correct. We'll load 4 and 4 values,
add them, store them back. But then, to have the correct behavior, we have to load only 1 and 1 values, add them and store back one value.
To account for such situations, usually the one loop becomes a two-part thing. The first part is sort of what we wrote above,
which is the vectorized version of the loop and runs as long as more than VF (where VF is the vectorization factor)
steps remain to be done. For example, for VF = 4, we would continue to execute the loop as long as there are more
than (or equal to) 4 steps to do. It would look like this (note that I don't actually use code such as if (i >= 4) ...):
void sum_arrays(int *A, int *B, int *C, int len) { int end = (len % 4 == 4) ? len : len - 4; for (int i = 0; i < end; i += 4) { __m128i v1 = loadu_si128(&A[i]); __m128i v2 = loadu_si128(&B[i]); __m128i res = add4(v1, v2); store_si128(&C[i], res); } }
Another faster way to compute end is to do: len & -4. Notice that -4 has all the bits set except the least significant 2. Also notice that any multiple of 4 has the least significant 2 bits unset. This operation "crops" the 2 least-significant bits, which means that it will round down len to the nearest multiple of 4. That works for any power of 2 (because any multiple of a 2m power will have the last m bits unset)
Now, we just need some code to handle any "remainder" iterations. Usually, this is the scalar (original) version of the loop:
void sum_arrays(int *A, int *B, int *C, int len) { int end = (len % 4 == 4) ? len : len - 4; int i = 0; for (; i < end; i += 4) { __m128i v1 = loadu_si128(&A[i]); __m128i v2 = loadu_si128(&B[i]); __m128i res = add4(v1, v2); store_si128(&C[i], res); } for (; i < len; ++i) { C[i] = A[i] + B[i]; } }
Some series of operations can be repeated and have the same result. For instance, the series
"load from memory X and Y, add them, store it into Z" (which is basically what every iteration / step does) can
be repeated as many times with the same result stored into Z. So, in that case, the remainder part instead of
being a scalar loop, can be a single vectorized operation that repeats some of the iterations while also
handling the remainder ones. For example, imagine again that len == 5.
We can do the first 4 iterations at once in the first loop, and then, to handle the last iteration, we can
do 4 iterations vectorized, but starting from the second iteration (5 - 4 = 1, the second iteration).
It's like you have a moving window with width of 4 and you move it 4 places at a time (doing 4 iterations at once every time). For the remainder places (in the example, only one, as 5 - 4 = 1) you can put the window so that it covers them but of course it may cover again some previous places too. That's ok, if the series of operation that you do can be repeated and so, it's ok to be repeated for these places that you cover again. Here's this version:
void sum_arrays(int *A, int *B, int *C, int len) { int end = (len % 4 == 4) ? len : len - 4; int i = 0; for (; i < end; i += 4) { __m128i v1 = loadu_si128(&A[i]); __m128i v2 = loadu_si128(&B[i]); __m128i res = add4(v1, v2); store_si128(&C[i], res); } // Last 4 iterations and we may repeat some. int index = len - 4; __m128i v1 = loadu_si128(&A[index]); __m128i v2 = loadu_si128(&B[index]); __m128i res = add4(v1, v2); store_si128(&C[index], res); }
Since we're copying a lot of code here, it would also make sense to create a wrapper function.
More correctness problems arise when the pointers alias. Imagine
that there's a buffer of allocated memory and A points to the first element,
B to the third (so B[0] is the third element of the buffer)
and C to the fifth.
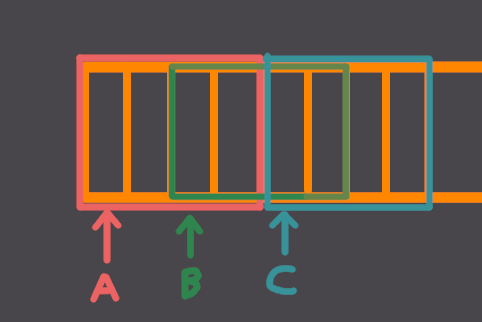
If we know try to do one vectorized iteration of the loop, we will read 4 elements from A
and 4 from B. Note that in the 4 elements of B,
there will be 2 elements of C, because B[2], B[3] are
also the elements C[0], C[1]. Now, in the scalar version, we first write
into C[0] in the first iteration and then we read from it (using B[2])
in the third iteration. But in the vectorized version, we will read the old value of B[2] (i.e.
whatever was there before), before writing into it and that's obviously wrong.
There are two main ways to tackle this: One way is to put run-time checks that ensure that the 3 pointers don't alias and if they do, jump into the scalar version of the loop:
void sum_arrays(int *A, int *B, int *C, int len) { if (A + len > Β) jump to the scalar version if (B + len > A) jump to the scalar version ... }
This is what the compiler will do if it tries to vectorize a loop. The other way is to use the keyword in the pointer arguments restrict. There are a lot to say about this keyword (and I have said some) but for a pointer function argument, it just means "trust me, this pointer does not alias with any other pointer in the function". But you have to make that clear to the user of the function.
In the next part, we see how to vectorize one of the most common vectorization suspects: reductions.